Beer-Lambert’s law proves a direct correlation between the absorbance (A) of a molecule to the concentration (c) and the path length (b) of the sample as has been observed in the article for the Derivation of Beer Lambert Law. This relationship is a linear for the most part. However, under certain circumstances the Beer Lambert relationship breaks down and gives a non-linear relationship. These deviations from the Beer Lambert law can be classified into three categories:
- Real Deviations – These are fundamental deviations due to the limitations of the law itself.
- Chemical Deviations– These are deviations observed due to specific chemical species of the sample which is being analyzed.
- Instrument Deviations – These are deviations which occur due to how the absorbance measurements are made.
I shall attempt to clarify each of these with suitable examples so as to improve your understanding of spectroscopy.
Real Limitation and Deviation of Beer-Lambert Law
Beer law and Lambert law is capable of describing absorption behavior of solutions containing relatively low amounts of solutes dissolved in it (<10mM). When the concentration of the analyte in the solution is high (>10mM), the analyte begins to behave differently due to interactions with the solvent and other solute molecules and at times even due to hydrogen bonding interactions.
- At high concentrations, solute molecules can cause different charge distribution on their neighboring species in the solution. Since UV-visible absorption is an electronic phenomenon, high concentrations would possibly result in a shift in the absorption wavelength of the analyte. At times, even electrolyte concentrations (such as those present in buffers) play an important role in altering the charge distributions and affecting UV-visible absorbance. Some large ions or molecules show deviations even at very low concentrations. For e.g. methylene blue absorptivity at 436 nm fails to observe Beer Lambert law even at concentrations as low as 10μM.
- High analyte concentrations can also possibly alter the refractive index (η) of the solution which in turn could affect the absorbance obtained. If the addition of solute causes a significant change in the refractive index of the solution a correction to the Beer Lambert formula can be placed as:
A = εbc (η2 + 2)2
This correction is normally not required below concentrations of 10mM.
Chemical Deviations and Limitations to Beer-Lambert Law
Chemical deviations occur due to chemical phenomenon involving the analyte molecules due to association, dissociation and interaction with the solvent to produce a product with different absorption characteristics. For example, phenol red undergoes a resonance transformation when moving from the acidic form (yellow) to the basic form (red). Due to this resonance, the electron distribution of the bonds of molecule changes with the pH of the solvent in which it is dissolved. Since UV-visible spectroscopy is an electron-related phenomenon, the absorption spectrum of the sample changes with the change in pH of the solvent.
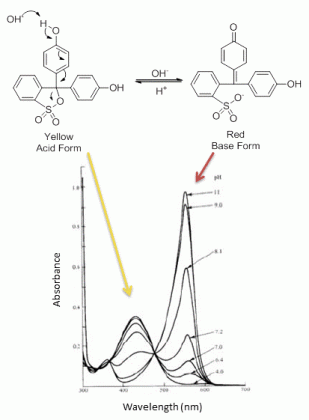
Instrumental Deviations and Limitations to Beer-Lambert Law
A] Due to Polychromatic Radiation (Also the reason why absorbance measurements are taken at the wavelength of maximum absorbance λmax)
Beer-Lambert law is strictly followed when a monochromatic source of radiation exists. In practice, however, it is common to use a polychromatic source of radiation with continuous distribution of wavelengths along with a filter or a grating unit (monochromators) to create a monochromatic beam from this source. For example (see figure below), consider a molecule having molar absorptivities ε’ and ε” at wavelengths λ’ and λ”. The absorbance (Am) for such a species can be calculated as:
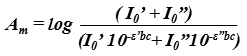
When the molar absorptivities are the same at both wavelengths (i.e. ε’ = ε”) , the relationship between absorbance and concentration follows Beer-Lambert law to obtain a straight line. However, as the difference between ε’ and ε” increases, the deviations from linearity also increases.
Why absorption measurements are taken at wavelength of maximum absorbance λmax?
If the band of wavelength selected on the spectrometer is such that the molar absorptivities of the analyte is essentially constant, deviations from Beer-Lambert law are minimal. However, if a band is chosen such that the molar absorptivity of the analyte at these wavelengths changes a lot, the absorbance of the analyte will not follow Beer-Lambert law. It is observed (as demonstrated in the figure below) that the deviations in absorbance over wavelengths is minimal when the wavelength observed is at the λmax. Due to this reason absorption measurements are taken at wavelengths.
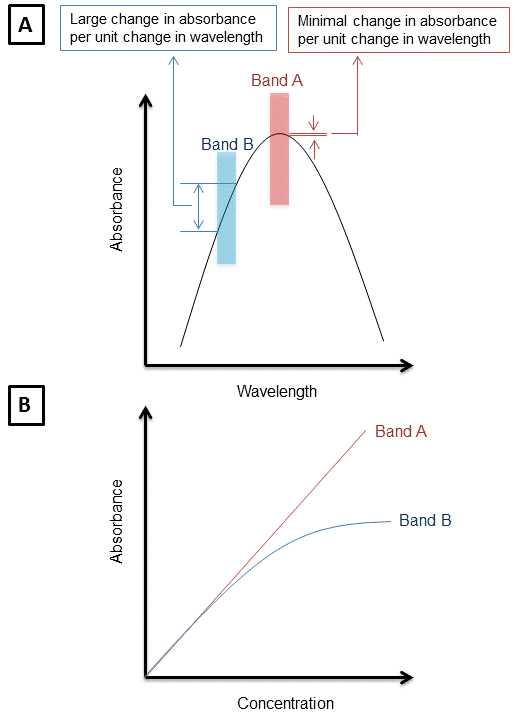
B] Due to Presence of Stray Radiation
Stray radiation or scattered radiation is defined as radiation from the instrument that is outside the nominal wavelength band selected. Usually the wavelength of the stray radiation is very different from the wavelength band selected. It is known that radiation exiting from a monochromator is often contaminated with minute quantities of scattered or stray radiation. Usually, this radiation is due to reflection and scattering by the surfaces of lenses, mirrors, gratings, filters and windows. If the analyte absorbs at the wavelength of the stray radiation, a deviation from Beer-Lambert law is observed similar to the deviation due to polychromatic radiation.
C] Due to Mismatched Cells or Cuvettes
If the cells holding the analyte and the blank solutions are having different path-lengths, or unequal optical characteristics, it is obvious that there would be a deviation observed in Beer-Lambert law. In such cases when a plot of absorbance versus concentration is made, the curve will have an intercept k and the equation will be defined as:
A = εbc + k
In today’s instrument this problem is generally not observed, however if it is present, appropriate linear regression to quantify this deviation must be made.
References
- Analytical Chemistry: An Introduction (Saunders Golden Sunburst Series) 7th Ed., by Douglas A. Skoog, Donald M. West, F. James Holler. 1999.
- Practical Pharmaceutical Chemistry 4th Ed. Edited by A. H. Beckett and J. B. Stenlake. 1988.
- Fundamentals of Analytical Chemistry 8th Ed., by Douglas A. Skoog, Donald M. West, F. James Holler, Stanley R. Crouch. 2003.
- Brian Lamp, Lecture notes Chemistry 322. UV-Vis Techniques. (accessed on 13th May, 2012).

a work well done, thanks
Hi
by increasing wavelength, the absorbance also increases until a maximum .after then relation is reverse, why?
are there any other conditions such as symmetry of the molecule which need to be satisfied for the uv to work.
Helpful ????
Hi,
Thanks for a good derivation, and summary about the deviations.
In Non Dispersive IR gas sensors, the HBW of the optical filters used typically is tens of nanometers. On the other hand, the absorption peak of a gas consists of adjacent narrow absortption spikes. This leads to considerable deviations from Beer’s law already in the normal measured cobcentrations.
For example, in a sensor for CO2 concentrations in breathing gases (up to 15 vol%) the concentration is calculated by c= k*A^1.4 when the CWL of the optical filter is 4.27 um and HBW is 80 nm.
As you know, the optical path length through the sample is important to be optimized for optimal signal to noise ratio of the measurement (at the most important concentration of the analyte). Too short a path length leads to small absorbances tedious to measure and too long a path leads to weak intensity on the detector, causing the detector noise to become a nuisance.
Wel treated,tnx
It is completely explained. Kudos
2.It is also possible that the concentration is so high, that the molecules create a screen for other molecules thereby shadowing them from the incident light.
Might want to elaborate on this part if you get a chance. I could think of FRET as a type of example.
Nice article.
Hi Rob,
FRET is off course slightly different as it uses fluorescence but the idea of local concentrations is well understood for people who understand FRET. Thanks for the compliment. I hope to write similar articles (possibly with animation) for fluorescence in the future.
I agree with Rob, It would be good with an elaboration of that part; e.g. how high an concentration (or how long the path length trough the sample) can be, before measurable deviations appear. Of course this would be instrument dependent, but a rule of thumb or a formula would be great.
I suppose it would be also dependant on the absorptivity of the molecule. This could make for someone’s thesis if the work is already not done :).
Not really. Hopefully by the time they start doing a thesis they know that this is wrong. The derivation of the Beer Lambert law requires screening to produce an exponential decay of intensity. If no screening occurred it would be a linear decay.
Unless you meant concentrations that are so high only a few photons are actually passing through the material.
Hi Jeff,
I did mean at high concentrations by stating the term “so high”.
Regards.