Blog

Click Here To View Presentation

Note- Subscripts are not correctly put by the website in all places. Terms such as DB are actually DB and could not be changed throughout the page. Kindly adjust accordingly.

Abstract:

Absorption is characterized by evaluating the absorption rate constant ka from plasma concentration versus time data graphs. Most pharmacokinetic models assume first order kinetics for the oral absorption of the drug; however zero-order assumption can also occur…

The rate of change of drug in the body at any time is equal to the amount of drug absorbed and the amount of drug eliminated from the body at any time, regardless of whether the absorption is first-order or the second order. A plasma-level time curve showing drug absorption and elimination can be made.

Zero-order drug absorption from the dosing site into the plasma occurs when a zero-order controlled release delivery system is used. This model is analogous to that of administration of drug by intravenous infusion.
Normally absorption process in the body is assumed to follow first-order kinetics. This model applies to the drugs those are in solution form or rapidly dissolving dosage forms.

Absorption rate constant can be determined by the “METHOD OF RESIDUALS” by plotting the oral absorption data. In One-Compartment Model, by plotting amount of drug absorbed versus time or by plotting the amount of drug unabsorbed versus time;Using both plasma and urinary data. And also in Two-Compartment Model (loo-reigelman method),by plotting the amount of drug unabsorbed vs. time.

In few individuals, the absorption of drug after a single oral-dose does not start immediately, Due to some physiological factors as stomach-emptying time and intestinal motility, the time delay prior to the commencement of first-order absorption is the lag-time.

Using the method of residuals to estimate ka and kel, the terminal phase of the absorption curve is usually represented by kel whereas steeper slope is represented by ka .In few cases kel obtained from oral absorption does not agree with that obtained after I/v bolus. Apparently the ka and kel obtained by this method has been interchanged. This phenomenon is termed as “flip-flop” of ka and kel.

The plot of the fraction unabsorbed against t, using blood data, yields the slope-ka/2.303.If this graph gives a linear regression; hence the rate of drug absorption DGI/ Dt is a first-order process. Similarly a graph of this fraction of drug unabsorbed vs. time can be made using urinary data as well. And the slope of this curve represents the absorption-rate constant. From this method an accurate measurement of absorption-rate constant can be made.

In two-compartment method also, the amount of drug unabsorbed vs. time can be plotted and accurate ka-determination can be done but the limitation in this method is that the determination of ke is first made by giving the same drug I/vly. The drugs that can’t be given orally, their ka can’t be determined by this method.So determination of absorption rate constant is a very important measure when comparing the bioavailability of the drug in bioequivalence studies.

Drug absorption:

“Absorption is defined as the appearance of drug in the body fluids.”

Kinetics of oral absorption of drug:

Absorption is characterized by evaluating the absorption rate constant ka from plasma concentration versus time data graphs. Most pharmacokinetic models assume first order kinetics for the oral absorption of the drug; however zero-order assumption can also occur.

Schematically:

Mathematically:

The rate of change of drug in the body at any time is equal to the amount of drug absorbed and the amount of drug eliminated from the body at any time, regardless of whether the absorption is first-order or the second order.

dDB/dt = dDG/dt – dDE/dt
DG = drug at the absorption site (gut)
DB = drug in the body
DE = eliminated drug
ka = first-order absorption rate constant
ke = overall elimination rate constant

Graphically:

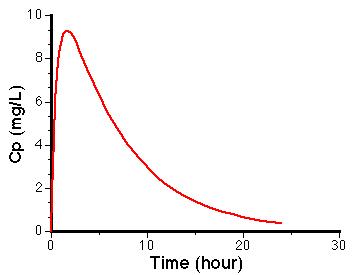
A plasma-level time curve showing drug absorption and elimination can be made.

Absorption phase:
Rate of drug absorption is greater than the rate of drug elimination.  dDG/dt >  dDE/dt
Peak-drug concentration:
Rate of drug absorption equals rate of drug elimination.                    dDG/dt = dDE/dt
Post-absorption phase:
Rate of drug absorption at this time is faster than the rate of absorption.     dDG/dt <  dDE/dt
Elimination phase:
Drug absorption appears zero. The plasma level time curve only represents the rate of drug elimination.
dDB/dt =-kDB

ABSORPTION MODELS:

Absorption can follow both zero-order and first-order absorption models.

1. Zero order absorption models.:

Zero-order drug absorption from the dosing site into the plasma occurs when a zero-order controlled release delivery system is used. Here drug DG is absorbed systemically at a constant rate,k0 and is simultaneously and immediately eliminated from the body by a first-order rate constant , k .this model is analogous to that of administration of drug by intravenous infusion.

Schematically:

Mathematically:

The rate of drug input is k0 and the rate of drug elimination is k. Therefore net change per unit time in the body is:
dDB/dt = -kDB
As DB=VdCp so integrating the equation  Cp=k0/Vdk(1-e-kt)
The rate of change of drug absorption is constant until the amount in the gut , DG is depleted. Time for complete drug absorption is DGI/k0 after this time drug is no longer available for absorption from the gut and then the drug declines in the plasma following the 1st-order elimination rate process.

2. First-order absorption model:

Normally absorption process in the body is assumed to follow first-order kinetics. This model applies to the drugs those are in solution form or rapidly dissolving dosage forms.

Differential Equations:

The differential equations describing the rates of change of the three components DG, DB and DE are:

(1)    the rate of disappearance of drug from the gut:

dDG/dt = -kaDGF  (where F is the fraction absorbed)

(2)   the rate of drug change in the body is the rate of drug in – the rate of drug out of the body:

dDB/dt =F kaDG – kelDB

(3)    the rate of drug elimination:

dDE/dt = +kelDB

dDB/dt =FkaDG-kelV.Cp     (DB=V.Cp)

The first term, ka •DG, represents absorption and the second term, kel.V.Cp, represents elimination.
Using Laplace transforms, our equation becomes:

where [(DGOka)/(ka-kel)] represents the amount of drug in the body through extra vascular administration.  The two exponential terms represent elimination[exp(-kelt)] and absorption[exp(-kat)] of the drug.  By dividing both sides by Vd which is the apparent volume of distribution, we obtain the concentration of the drug within plasma versus time.

Graphically:

A typical plot of drug in the body after a single dose is constructed.

Shortly after the dose is administered DG is much larger than V• Cp therefore the value of V • dCp/dt is positive, therefore the slope is positive and Cp will increase. With increasing time after the dose is administered, DG will decrease, while initially Cp is increasing, therefore there will be a time when ka • DG will equal kel • V • Cp. At this time V • dCp/dt will be zero and there will be a peak in the plasma concentration. At even later times DG will approach zero, and V • dCp/dt will become negative and Cp will decrease. It could be expected that the plasma concentration time curve will look like this.

It is apparent that the right hand side of this equation is a constant multiplied by the difference of two exponential terms. A biexponential equation.

Absorption rate constant

“It may be described as a value describing how much drug is absorbed per unit of time”.

Determination of absorption rate constant:

Absorption rate constant can be determined by the “METHOD OF RESIDUALS” by plotting the oral absorption data.

1.In One-Compartment Model

A .by plotting amount of drug absorbed versus time

B .by plotting the amount of drug unabsorbed versus time

a.by.using plasma-data.
b.by using urinary data.

2.In Two-Compartment Model.

Method of residuals

Each will e discussed below:

1.In One-Compartment Model:

A. Amount of drug absorbed vs. time:
Using the equation

From this equation we can get the y-intercept.as with the passage of time, drug absorption is virtually complete so exp(-kat)=0

As

Steps involved in method of residuals:
This equation representing the first-order drug elimination will yield a linear plot on semi log paper. This slope is equal to –k/2.303.The value of ka can be obtained using the method of residuals, or feathering technique by the following procedure:
1.Plot the drug-concentration versus time, with time on x-axis and conc. on y-axis.
2.Obtain the slope of the terminal phase by extrapolation
3.Take any points on the upper part of the line(x1,x2,and x3) and drop vertically to obtain corresponding points on the curve(x’1,x’2,x’3)
4.Read the conc. values at x1 and x’1 and so on and plot the difference at the corresponding time point’s t1,t2,t3.a straight line will be obtained with a slope of –ka/2.303.

• When using the method of residuals, the minimum of three points should be used to define the line and data points shortly after tmax shouldn’t be used as this is post-absorption phase. Only data points from the elimination phase should be used to define the rate of drug absorption as a first-order process.
• If drug absorption occurs immediately after oral administration, then the residual lines obtained will intersect on y-axis at point A. this represents a hybrid constant composed of ka,kel,V d and FD0

Lag-time: In few individuals, the absorption of drug after a single oral-dose does not start immediately, Due to some physiological factors as stomach-emptying time and intestinal motility, the time delay prior to the commencement of first-order absorption is known as lag-time.
Lag-time is observed when the oral-absorption curve intersects at some point greater than t=0.Time at the point of intersection on x-axis is the lag-time.and it represents the beginning of drug absorption..

Flip-Flop Of Ka And Kel:

Using the method of residuals to estimate ka and kel, the terminal phase of the absorption curve is usually represented by kel whereas steeper slope is represented by ka .In few cases kel obtained from oral absorption does not agree with that obtained after I/v bolus. Apparently the ka and kel obtained by this method has been interchanged. This phenomenon is termed as “flip-flop” of ka and kel.

So in order to demonstrate that the steeper curve represents kel for a drug given extravescularly, drug must be given I/vly into the same patient. After I/v inj. Decline in the plasma-level time curve represents the true-elimination rate.

Drugs having flip-flop characteristics: are generally the one that have fast elimination.(ke>ka).so for drugs with large kel, the chance of flip-flop is much greater.

B. Fraction of drug un-absorbed vs. time: (Wagner-Nelson Method)

1.From Blood-Data:

After a single oral dose of drug, dose is expressed by
D0=DGI+DB+DU
Let Ab = DB+DU (amount of drug absorbed)   And Ab∞=amount of drug absorbed at t∞
And so at any time the amount of drug absorbed is Ab/Ab∞
And the fraction of drug unabsorbed is (1- Ab/Ab∞)
Amount of drug excreted at any time is
DU=kVD[AUC]t 0           and                 DB=CpVD
SO                   Ab= CpVD+ kVD[AUC]t 0
Ab∞=0+ kVD[AUC]∞ 0                as at t=∞,Cp∞=0
So the fraction of drug absorbed is
Ab/Ab∞= CpVD+ kVD[AUC]t 0/ kVD[AUC]∞ 0
=Cp+k[AUC]t 0/ k[AUC]∞ 0
And the fraction of drug unabsorbed is
(1- Ab/Ab∞)=1-( Cp+k[AUC]t 0/ k[AUC]∞ 0  )
The drug remaining in the GIT at any time t is:
DGI=D0e-kat             and          DGI/ D0= e-kat
log DGI/ D0=-kat/2.303 (taking log)
as DGI/ D0is actually the fraction of drug unabsorbed that is (1- Ab/Ab∞), so the plot of this fraction unabsorbed against t yields the slope-ka/2.303.
Steps in determination of ka:
1. Plot the fraction of drug unabsorbed vs. time.
2. Find k from the terminal part of the slope when the slope is –k/2.303.
3. Find [AUC]0t by plotting Cp vs. t.
4. Find k[AUC]0t  by multiplying each [AUC]0t with k.
5. Find all [AUC]∞t by adding up all [AUC]0t from t=0 to t=∞
6. Determine (1- Ab/Ab∞)
7.  Plot this (1- Ab/Ab∞) vs. time on semi log graph paper with (1- Ab/Ab∞) on y-axis.
If this graph gives a linear regression. Then the rate of drug absorption DGI/ Dt is a first-order process.

Advantages:
i) The absorption and elimination processes can be quite similar and still accurate determinations of ka can be made.
ii) The absorption process doesn’t have to be first order. This method can be used to investigate the absorption process. This type of method has been used to investigate data obtained after IM administration and it was found that two absorption steps maybe appropriate. Possibly a fast step from drug in solution and a slower step from drug precipitated at the injection site.
Disadvantages:
i) The major disadvantage of this method is that you need to know the elimination rate constant, from data collected following intravenous administration.



2.From the Urinary Data:

Absorption rate constant can also be determined from urinary-excretion data using the plot of amount of drug un-absorbed vs. time.
dAb = DB+DE
Differential of this equation gives
d Ab/dt =d DB/dt+dDE/dt        1
Assuming first-order kinetics for elimination constant ke
dDU/dt=keDB= ke VDCp,
Rearranging this equation and taking differential :
dCp/dt=d (dDU/dt)/ ke VDdt
Substituting all these values in the above equation 1 we get
d Ab/dt= d (dDU/dt)/ ke dt+k/ke( DdU/dt)
and when the above equation is integrated from 0-∞ ,
Ab/t= 1/ke (dDU/dt)+k/ke(dDU)t
At t=∞, all the drug that is ultimately absorbed is expressed as Ab∞  and dDU/dt=0.so the total amount of drug absorbed is :
Ab∞= k/ke×(DU)∞
where Du∞is the amount of drug excreted unchanged in the urine.
And so the fraction of drug absorbed is
Abt/ Ab∞=(dDU/dt)+k(DU)t /kDU∞
And a plot of the fraction of drug unabsorbed (1- Abt/ Ab∞),vs. t gives –k/2.3 as a slope from which the absorption rate constant can be determined.

2. In Two-Compartmental Model (Loo-Riegelman Method):

Plotting the percent of drug unabsorbed vs. time can be used for two-compartment model as well. This method requires that the drug is given i/v and orally.
After given the dose of the drug orally, the amount of drug absorbed is calculated as a sum of the amounts of drug in the central compartment plus tissue compartment and the amount of drug eliminated by all routes.

Total amount of drug in the body : Ab=Dp+Dt+Du
As        Dp=VpCp          , Dt=VtCt        ,    dDu/dt=kVpCp ,     Du=kVp[AUC]0t
Substituting these values for Dp, Du we get amount of drug in the body.i.e.
Ab= VpCp +Dt+ kVp[AUC]0t
Dividing this equation by Vp
Ab/Vp= Cp +Dt/Vp+ k[AUC]0t
At t=∞,this equation becomes,
Ab∞/Vp= k[AUC]0∞
Dividing both equations we get
Ab/Ab∞=( Cp +Dt/Vp+ k[AUC]0t)/  k[AUC]0∞
A plot of this fraction of drug unabsorbed vs. time gives the slope –ka/2.303 from which the
value of absorption rate constant is determined. Cp and [AUC]0t are calculated from the plot of
Cp vs. t .And the values of Dt/Vp can be approximated by Loo-Riegelman method is given by:
(Ct)tn=(k12∆Cp∆t)/2 + k12/k21(Cp)tn-1(1-e-k21∆t) = (Ct)tn-1 e-k21∆t
Where Ct=apparent tissue conc.
t=time of sampling for sample n.
tn-1=time of sampling for the sampling point preceding sample n.
(Cp)tn-1=conc of drug at central compartment for sample n-1.

Limitation: For calculation of ka by this method, the drug must be given i/v to allow evaluation of the distribution and the elimination rate constants .For the drugs that cannot be given i/v, ka cannot be calculated by Loo-Reiegelman Method. So for those drugs, Wagner-Nelson method may be used that assumes ka in one-compartment model.

Effects of Absorption-Rate Constant:

Higher the absorption rate constant, faster the absorption of the drug. As the peak concentration is a function of both the rate of absorption and the rate of elimination. If the elimination rate is the same, as the absorption rate increases, the peak concentration increases. And the product with highest peak conc, will exhibit highest intensity of effects. so

• If the value for ka and kel are reversed ,tmax is same but Cmax and AUC are different.
• If kel is constant and only ka is increased, then tmax becomes shorter and Cmax is increased and AUC remains same.
• And if ka is kept constant but ke is increased, then tmax ,Cmax and AUC decreases.
• For many immediate-release dosage forms, the absorption process is first-order due to the physical nature of drug diffusion.
• The calculation of ka is useful in designing a multiple-dosage regimen.
• Knowledge of ka and k allows for the prediction of peak and trough plasma drug concentrations following multiple dosing.
• In bio-equivalent studies, time of peak concentrations can be very useful in comparing respective rates of absorption of a drug from chemically equivalent drug products.

Significance of Absorption-Rate Constant:

• For many immediate-release dosage forms, the absorption process is first-order due to the physical nature of drug diffusion.
• The calculation of ka is useful in designing a multiple-dosage regimen.
• Knowledge of ka and k allows for the prediction of peak and trough plasma drug concentrations following multiple dosing.
• In bio-equivalent studies, time of peak concentrations can be very useful in comparing respective rates of absorption of a drug from chemically equivalent drug products.

References

• Applied Biopharmaceutics and Pharmacokinetics by Leon Shargel.Chapter no.7,page no.161.
• Pharmacology and Experimental Therapeutics Department Glossary at Boston University School of Medicine.
• Journal of Pharmacokinetics and Pharmacodynamics, Volume 8, Number 2 / April, 1980, pages 203-214.
• Mayersohn, M and Gibaldi, M. 1970 Mathematical Methods in Pharmacokinetics. I Use of the Laplace Transform for Solving Differential Rate Equations, Amer. J. Pharm. Education, 34, 608-614
• http://www.boomer.org/c/p3/c17/c1704.html
• Mosby’s Medical Dictionary, 8th edition. © 2009, Elsevier.
• http://mips.stanford.edu/public/classes/pharmacokinetics/2006/Lin_comp/MDR/RepDosing2ab.html
• Gibaldi, M.; Perrier, D. Pharmacokinetics, 2nd Edition, Volume 15. Drugs and The Pharmaceutical Sciences
• http://www.boomer.org/c/p1/Ch09/Ch0903.html