Note- If you have any questions post them in the comments section below and we will put up those problems in this article.
Introduction
It is always challenging when someone asks you to calculate the concentrations or make new concentrations of solutions in labs or classrooms. Being pharmacy and pharmaceutical science students, we face concentrations all around us in some form or the other. This article is aimed to guide you better on how you can do the calculations and understand what is going on while calculating concentrations. We start off with the definition of Avagadro’s Number, cover gram molecular weight, moles, molarity etc. and will end with real life example problems with solutions which you can use to practice your calculations with.
Avagadro’s Number
The Avagadro Constant or Avagadro’s Number is named after the Italian scientist Amedeo Avagadro [1]. He proposed that the volume of gas (at a given pressure and temperature) is proportional to the number of molecules present, regardless of the nature of the gas. It was the French physicist Jean Perrin who named the constant after Avagadro in his honor [2].
Back to the Basics
Before we start we must know what is Dalton, molecular weight and gram-molecular weight.
Dalton (Da) is a unit that is used for indicating mass on an atomic and molecular scale. 1 Da is approximately equal to the mass of 1 proton or 1 neutron. However, a correct measure of Daltons is done with respect to carbon-12 and is 1/12th the mass of an unbound atom of C12 in its ground state. Therefore 1Da = 1/12 the mass of 1 carbon-12 atom.
Molecular mass of a molecule is- as the term suggests, the mass of each atom or molecule. For e.g. Carbon has a total of 12 nucleons (protons + neutrons). Since 1Da is the weight of one nucleon (either 1 proton or neutron), the molecular weight of carbon is 12. E.g. 2. Water has two hydrogens and one oxygen. The oxygen atom has 16 nucleons, while the two hydrogens have 1 nucleon each. The total number of nucleons in the water molecule is 18, and since 1Da is the measure of 1nucleon, the molecular mass of water is 18Da.
Note – although, molecular mass and molecular weight have been used interchangeably in a number of places, they are not the same.
Gram molecular weight is the amount of molecular substance whose weight, in grams, is numerically equal to the molecular mass of the substance. It is basically a term used to make quantities of atoms and molecules measurable using daily instruments. For e.g. one gram-molecular weight of carbon is 12 grams and one gram molecular weight of water is 18 grams [3].
So what exactly is this Avagadro’s Number?
Avagadro’s Number is the number of molecules, atoms, or other elementary entities (like ions) in the gram molecular weight of the molecule. This number is a constant irrespective of the elementary entity. For e.g. molecular weight of molecular oxygen is 32 (as it has two oxygen atoms). Therefore, 32g (i.e. the gram molecular weight) of oxygen will contain Avagadro’s number of molecules in it. Similarly, molecular weight of carbon is 12, and 12g of pure carbon will contain Avagadro’s number of molecules in it. The value for Avagadro’s number is 6.023 x 1023 mol -1. What this means is that 32g of oxygen contains the same number of molecules as 12g of carbon and they both contain Avagadro’s number of molecules.
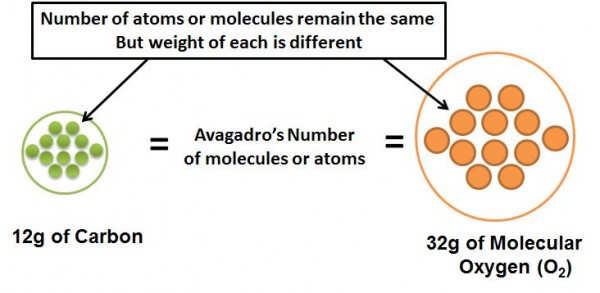
The unit mol -1 (or 1/moles) denotes that, that is the number of molecules in the gram-molecular weight of the molecule. Therefore the number of moles of a compound is the weight of the compound divided by the molecular weight. So say we had 24g of solid carbon (gram molecular weight is 12g), that would mean that we had 24/12 = 2 moles of carbon = 2 x Avagadro’s Number of Molecules.
How do we use Avagadro’s Number when calculating concentrations?
The answer is no. We never use Avagadro’s number while measuring concentrations directly. But what we do use is moles which in turn is a measure of the number of molecules and moles can be directly measured on the gram scale (i.e. can be used to weigh in the labs). The usage of moles in place of Avagadro’s Number is to make calculations easier. As seen above 1 mole = gram molecular weight of the molecule (thus can be weighed in the lab) = Avagadro’s number of molecules (thus we know the number of molecules in that much quantity of the molecule).
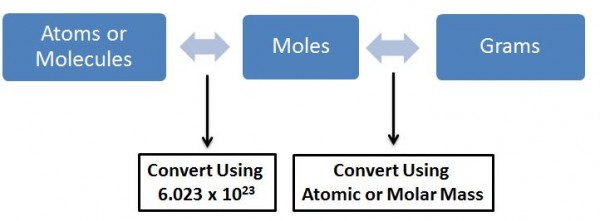
So how do we make a solution? All this is just weight of solids, liquids or gases?
When we make a solution, we have a solute and a solvent. A solute is the molecule which we are going to dissolve in a liquid. The liquid in which the solute is going to be dissolved is the solvent. What is important to us is the molecular weight of the solute. To make a one molar solution of the solute, you dissolve the gram-molecular weight of the solute in 1 litre (or 1000mL) of the solvent. Thus 1 litre of the solution will now have Avagadro’s Number of molecules in it of the solute. So supposing we had 46g of ethanol (solute), the molecular weight of ethanol is 46Da and the gram molecular weight is therefore 46 grams. If we dissolve this ethanol in 1000mL of water (our solvent), we will have a 1 molar solution of ethanol.
Note – Molarity is written as M. Thus, a 1 molar solution can be written as 1 M.
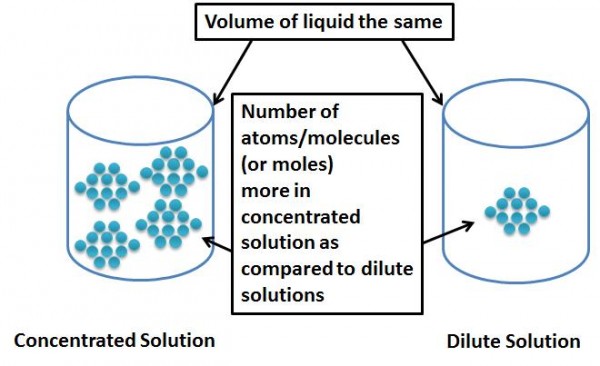
When we talk about concentrations of solutions, it is nothing but the proportion of the solute to that of the solution, i.e. the probability of finding a known quantity of solute, in a known volume of solvent or solution.
Concentration is Analogous to Density of the Solute in the Solution?
If you think about it, concentration is nothing but a measure of how many molecules of the solute are within the volume of solvent. If you add a lot of solute you get a more concentrated (or denser) solution. If you add more of solvent, you increase the space where solutes can move around so you are making a less concentrated (or more lighter or dilute) solution.
But what if we did not have 46 grams of ethanol and we added only 30grams of ethanol, what would be the concentration then?
In such a case we have less than 1 mole of the solute. So we calculate how many moles of solute we have. Therefore we divide the amount of solute we have by the gram molecular weight to get the number of moles i.e. 30/46 = 0.6527 moles. If we dissolve it in 1 liter of water we will have 0.6527 M solution.
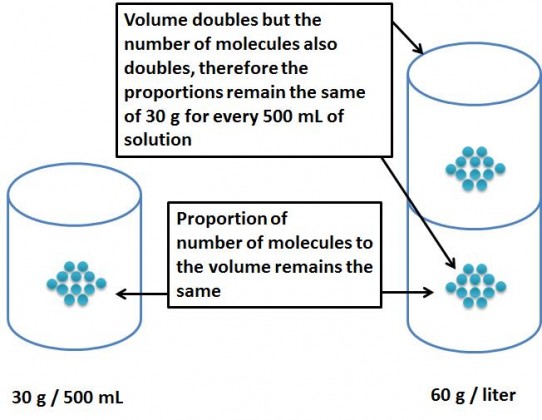
What if we dissolve the 30 grams of ethanol in 500mL of water?
Since now we are having lesser amount of solvent, the solute has lesser space to move around, and is therefore more concentrated. If we dissolve 30 grams in 500mL of water, the concentration (or density) of the solute would be the same as 60 grams in 1 Litre of water. Thus the weight per Liter of the solution would be equivalent to 60 grams per liter. If we divide this by the gram molecular weight we will get the concentration in terms of molarity. Therefore, the molar concentration of the solution is 60 g/L divided by the gram moleculare weight (46) which is = 1.304 M.
This is similar to making the concentration or making the solution more dense by decreasing the overall volume but keeping the solute quantity the same.
Why is 30g of ethanol in 500mL of water the same as 60g of ethanol in 1000mL of water?
This is because the “denseness” or the concentration remains unchanged, i.e. the proportion of the solute to the solution remains the same. This is the same reason why grams/liter can be readily converted to mg/mL.
We have a very concentrated solution – Now How Do We Make Dilutions?
Suppose, you have a highly concentrated solution (also known as a stock solution), for e.g. 1 litre of 1M solution. Now you would like to make 100mL of a 0.1M solution from this. Where would you begin.
Begin this way –
- What do we know?
We know we have 1 litre of 1M solution
We know that we want to make 100mL of 0.1M solution
- What is the unknown?
We want to know how much volume of 1M solution should we take and dissolve to make 100mL of solution to get 0.1M solution of 100mL
- How do we calculate?
This calculation involves a simple formula denoted by:
M1V1 = M2V2
Where M1 is the Molar concentration of the more concentrated solution (1M). V1 is the volume to be taken of the more concentrated solution (the unknown). M2 is the molar concentration of the more dilute solution which we would like to prepare (0.1M) and V2 is the volume of the more dilute solution which we would like to have at the end (i.e. 100mL). And the amount of solvent to be added in order to get the dilute solution to V1 is = V2 – V1.
So substituting the values in the above equation we get
1 x V1 = 0.1 x 100
Therefore,
V1 = 10mL and thus the amount of solvent to be taken = 100-10 = 90mL
So if we were to take 10mL of the more concentrated solution of 1M and add 90mL of the solvent we would get a total of 100mL of the 0.1M solution.
Note- the formula M1V1 = M2V2 is very important while making dilutions.
Note- when using M1V1 = M2V2 please keep the units on both the sides the same, i.e. if V1 is in mL, then V2 will also be in mL, and if M1 is in molar concentration, M2 will also be in molar concentration.
What is mole fraction and mole %?
The mole fraction X, denotes the number of moles of solute as a proportion of the total number of moles in a solution. For e.g. 1 mole of solute is dissolved in 9 moles of solvent, then the mole fraction would be 1/10. Since it is a ratio, mole fraction does not have any dimensions or units. If you multiply the mole fraction by 100 then what you get is the mole fraction in terms of a percentage or the mole %. Generally mole % is used to describe quantities of catalysts.
Formulas Worth Memorizing
1] Molarity = moles of solute / liters of solution
2] Molarity = (grams/liter of solute) / gram-molecular weight of solute
3] Molarity = (mg/mL of solute)/ gram-molecular weight of solute [note- here mg/mL is interchanged with g/L]
4] M1V1 = M2V2
Where M1 is the Molar concentration of the more concentrated solution. V1 is the volume to be taken of the more concentrated solution. M2 is the molar concentration of the more dilute solution which we would like to prepare and V2 is the volume of the more dilute solution which we would like to have at the end.
And the amount of solvent to be added in order to get the dilute solution to V1 is = V2 – V1.
Note- when using M1V1 = M2V2 please keep the units on both the sides the same, i.e. if V1 is in mL, then V2 will also be in mL, and if M1 is in molar concentration, M2 will also be in molar concentration.
Practical Applications of the Above Principles of Concentrations – Sample Problems:
1] Make a 5M solution of NaCl in water so that you have 500mL of the solution.
Solution:
1] We know – gram molecular weight of NaCl is 58.44. We have to make 5M solution of 500mL.
2] We don’t know – How many grams of NaCl we have to dissolve to get this solution.
3] How do we calculate?
If we dissolve gram-molecular weight of the compound in 1000mL of solvent we would get 1M solution.
If we dissolve 5 x gram-molecular weight of the compound in 1000mL we would get 5M solution.
However we do not need 1000mL we only want 500mL.
So for 500mL of solution we would need 1000/500 = 2 times lesser compound.
Therefore we would need 5 x gram-molecular weight / 2 of the compound in 500mL to get 5M solution of 500mL.
Therefore we would need to take 146.1 grams of NaCl and dissolve it in 500mL of water to make a 5M solution.
2] Take the 5M solution of NaCl in water and make a 2.5M solution in water so that you have 200mL of this solution.
Solution:
1] We Know – we have 500mL of 5M solution of NaCl in water. We want to make 2.5M solution of 200mL.
2] We don’t know- what volume of this 5M solution we need to take and the amount of water to be added to it so that it becomes 200mL of 2.5M solution.
3] How do we calculate?
Here we use the formula M1V1 = M2V2
M1 = 5M , V1= unknown, M2 = 2.5M, V2 = 200mL
Note- when using M1V1 = M2V2 please keep the units on both the sides the same, i.e. if V1 is in mL, then V2 will also be in mL, and if M1 is in molar concentration, M2 will also be in molar concentration.
Substituting above we get
5 x V1 = 2.5 x 200
Therefore, V1= 100mL and the amount of solvent to be taken is 200mL–100mL = 100mL
Thus we need to take 100mL of the 5M solution and add 100mL of water (solvent) to it to make 200mL of 2.5M solution.
If you have any questions post them in the comments section below and we will put up those problems in this article.
3] Someone in the lab has made a solution of 30g/L of NaCl solution in water. What is its concentration in terms of Molarity?
Solution:
1] We know – gram molecular weight of NaCl is 58.44g. Concentration of the solution in terms of g/L is 30 g/L.
2] We don’t know – concentration in Molarity
3] How do we calculate?
We can use the formula:
Molarity = (grams/Liter of solute)/ gram-molecular weight
i.e. = 30/58.44
=0.513M
The solution is therefore 0.513M solution.
References
- Avogadro, Amadeo (1811), “Essai d’une maniere de determiner les masses relatives des molecules elementaires des corps, et les proportions selon lesquelles elles entrent dans ces combinaisons”, Journal de Physique 73: 58–76. English translation.
- Perrin, Jean (1909), “Mouvement brownien et réalité moléculaire”, Annales de Chimie et de Physique, 8e Série 18: 1–114.Extract in English, translation by Frederick Soddy.
- http://www.infoplease.com/ce6/sci/A0821497.html
Note- If you have any questions post them in the comments section below and we will put up those problems in this article.